Automatic Differentiation for Python
Project description
ADiPy is a fast, pure-python automatic differentiation (AD) library. This package provides the following functionality:
Arbitrary order univariate differentiation
First-order multivariate differentiation
Univariate Taylor polynomial function generator
Jacobian matrix generator
Compatible linear algebra routines
Installation
To install adipy, simply do one of the following in a terminal window (administrative priviledges may be required):
Download the tarball, unzip, then run python setup.py install in the unzipped directory.
Run easy_install [--upgrade] adipy
Run pip install [--upgrade] adipy
Where to Start
To start, we use the simple import:
from adipy import *
This imports the necessary constructors and elementary functions (sin, exp, sqrt, etc.) as well as np which is the root NumPy module.
Now, we can construct AD objects using either ad(...) or adn(...). For multivariate operations, it is recommended to construct them all at once using the ad(...) function, but this is not required. The syntax is only a little more complicated if they are initialized separately.
Univariate Examples
Here are some examples of univariate operations:
# A single, first-order differentiable object x = ad(1.5) y = x**2 print y # output is: ad(2.25, array([3.0])) # What is dy/dx? print y.d(1) # output is: 3.0 z = x*sin(x**2) print z # output is: ad(1.1671097953318819, array([-2.0487081053644052])) # What is dz/dx? print z.d(1) # output is: -2.0487081053644052 # A single, fourth-order differentiable object x = adn(1.5, 4) y = x**2 print y # output is: ad(2.25, array([ 3., 2., 0., -0.])) # What is the second derivative of y with respect to x? print y.d(2) # output is: 2.0 z = x*sin(x**2) print z # output is: # ad(1.1671097953318819, array([ -2.04870811, -16.15755076, -20.34396265, 194.11618384])) # What is the fourth derivative of z with respect to x? print z.d(4) # output is: 194.116183837
As can be seen in the examples, when an AD object is printed out, you see two sets of numbers. The first is the nominal value, or the zero-th derivative. The next set of values are the 1st through the Nth order derivatives, evaluated at the nominal value.
Multivariate Examples
For multivariate sessions, things look a little bit different and can only handle first derivatives (for the time being), but behave similarly:
x = ad(np.array([-1, 2.1, 0.25])) y = x**2 print y # output is: # ad(array([ 1. , 4.41 , 0.0625]), array([[[-2. , 0. , 0. ], # [-0. , 4.2, 0. ], # [-0. , 0. , 0.5]]]))
This essentially just performed the **2 operator on each object individually, so we can see the derivatives for each array index and how they are not dependent on each other. Using standard indexing operations, we can access the individual elements of an AD multivariate object:
print x[0] # output is: # ad(-1, array([ 1., 0., 0.]))
What if we want to use more than one AD object in calculations? Let’s see what happens:
z = x[0]*sin(x[1]*x[2]) print z # output is: # ad(-0.50121300467379792, array([[ 0.501213 , -0.21633099, -1.81718028]]))
The result here shows both the nominal value for z, but also the partial derivatives for each of the x values. Thus, dz/dx[0] = 0.501213, etc.
Jacobian
If we have multiple outputs, like:
y = [0]*2 y[0] = x[0]*x[1]/x[2] y[1] = -x[2]**x[0]
we can use the jacobian function to summarize the partial derivatives for each index of y:
print jacobian(y) # output is: [[ 8.4 -4. 33.6 ] # [ 5.54517744 0. 16. ]]
Just as before, we can extract the first partial derivatives:
print z.d(1) # output is: [ 0.501213 -0.21633099 -1.81718028]
For the object y, we can’t yet use the d(...) function yet, because it is technically a list at this point. However, we can convert it to a single, multivariate AD object using the unite function, then we’ll have access to the d(...) function. The jacobian function’s result is the same in both cases:
y = unite(y) print y.d(1) # output is: [[ 8.4 -4. 33.6 ] # [ 5.54517744 0. 16. ]] print jacobian(y) # output is: [[ 8.4 -4. 33.6 ] # [ 5.54517744 0. 16. ]]
Like was mentioned before, multivariate sessions can initialize individual independent AD objects, though not quite as conveniently as before, using the following syntax:
x = ad(-1, np.array([1, 0, 0])) y = ad(2.1, np.array([0, 1, 0])) z = ad(0.25, np.array([0, 0, 1]))
This allows all the partial derivatives to be tracked, noted at the respective unitary index at initialization. Conversely to singular construction, we can break-out the individual elements, if desired:
x, y, z = ad([np.array([-1, 2.1, 0.25]))
And the results are the same.
Univariate Taylor Series Approximation
For univariate functions, we can use the taylorfunc function to generate an callable function that allows approximation to some specifiable order:
x = adn(1.5, 6) # a sixth-order AD object z = x*sin(x**2) fz = taylorfunc(z, at=x.nom)
The “at” keyword designates the point that the series is expanded about, which will likely always be at the nominal value of the original independent AD object (e.g., x.nom). Now, we can use fz whenever we need to approximate x*sin(x**2), but know that the farther it is evaluated from x.nom, the more error there will be in the approximation.
If Matplotlib is installed, we can see the difference in the order of the approximating Taylor polynomials:
import matplotlib.pyplot as plt
xAD = [adn(1.5, i) for i in xrange(1, 7)] # a list of ith-order AD objects
def z(x):
return x*sin(x**2)
x = np.linspace(0.75, 2.25)
plt.plot(x, z(x), label='Actual Function')
for i in xrange(len(xAD)):
fz = taylorfunc(z(xAD[i]), at=xAD[i].nom)
plt.plot(x, fz(x), label='Order %d Taylor'%(i+1))
plt.legend(loc=0)
plt.show()
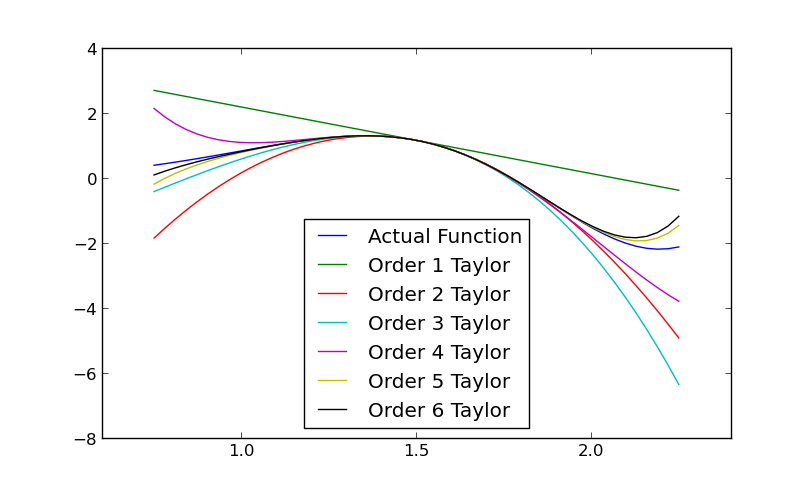
Notice that at x=1.5, all the approximations are perfectly accurate (as we would expect) and error increases as the approximation moves farther from that point, but less so with the increase in the order of the approximation.
Linear Algebra
Several linear algebra routines are available that are AD-compatible:
Decompositions
Cholesky (chol)
QR (qr)
LU (lu)
Linear System solvers
General solver, with support for multiple outputs (solve)
Least squares solver (lstsq)
Matrix inverse (inv)
Matrix Norms
Frobenius norm, or 2-norm (norm)
These require a separate import import adipy.linalg, then they can be using something like adipy.linalg.solve(...).
See the source code for relevant documentation and examples. If you are familiar with NumPy’s versions, you will find these easy to use.
Support
Please contact the author with any questions, comments, or good examples of how you’ve used adipy!
License
This package is distributed under the BSD License. It is free for public and commercial use and may be copied royalty free, provided the author is given credit.
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.











