Ordered subsets over a predefined domain
Project description
Bitsets are ordered sets which are subsets of a predefined finite domain of hashable items.
They are implemented as pure Python integers representing the rank of the set in colexicographical order (a.k.a bit strings, powers of two, binary strings). Hence, they can be very space-efficient, e.g. if a large number of subsets from a collection needs to be present in memory. Furthermore, they can be compared, intersected, etc. using normal bitwise operations of integers (&, |, ^, ~).
Installation
This package runs under Python 2.7 and 3.3+, use pip to install:
$ pip install bitsetsThere are no other dependencies. Optionally, you can install Graphviz and this Python wrapper for drawing Hasse diagrams (see below).
Creation
Use the bitset function to create a class representing ordered subsets from a fixed set of items (the domain):
>>> from bitsets import bitset
>>> Pythons = bitset('Pythons', ('Chapman', 'Cleese', 'Gilliam', 'Idle', 'Jones', 'Palin'))The domain collection needs to be a hashable sequence (e.g. a tuple).
The resulting class is an integer (int or long depending on Python version) subclass, so its instances (being integers) are immutable and hashable and thus in many ways similar to pythons built-in frozenset.
>>> from bitsets._compat import integer_types
>>> issubclass(Pythons, integer_types)
TrueThe domain items are mapped to powers of two (their rank in colexicographical order):
>>> Pythons.fromint(0)
Pythons()
>>> [Pythons.fromint(1), Pythons.fromint(2), Pythons.fromint(4)]
[Pythons(['Chapman']), Pythons(['Cleese']), Pythons(['Gilliam'])]
>>> Pythons.fromint(2 ** 6 - 1)
Pythons(['Chapman', 'Cleese', 'Gilliam', 'Idle', 'Jones', 'Palin'])
>>> Pythons.fromint((1 << 0) + (1 << 5))
Pythons(['Chapman', 'Palin'])The class provides access to the minimal (infimum) and maximal (supremum) sets from its domain:
>>> Pythons.infimum
Pythons()
>>> Pythons.supremum
Pythons(['Chapman', 'Cleese', 'Gilliam', 'Idle', 'Jones', 'Palin'])Basic usage
Bitsets can be created from members, bit strings, boolean sequences, and integers:
>>> Pythons(['Palin', 'Cleese'])
Pythons(['Cleese', 'Palin'])
>>> Pythons.frombits('101000')
Pythons(['Chapman', 'Gilliam'])
>>> Pythons.frombools([True, False, True, False, False, False])
Pythons(['Chapman', 'Gilliam'])
>>> Pythons.fromint(5)
Pythons(['Chapman', 'Gilliam'])Members always occur in the definition order.
Bitsets cannot contain items other than those from their domain:
>>> Pythons(['Brian'])
Traceback (most recent call last):
....
KeyError: 'Brian'Bitsets can be converted to members, bit strings, boolean sequences and integers:
>>> Pythons(['Chapman', 'Gilliam']).members()
('Chapman', 'Gilliam')
>>> Pythons(['Chapman', 'Gilliam']).bits()
'101000'
>>> Pythons(['Chapman', 'Gilliam']).bools()
(True, False, True, False, False, False)
>>> int(Pythons(['Chapman', 'Gilliam']))
5Sorting
To facilitate sorting collections of bitsets, they have key methods for different sort orders (shortlex, longlex, shortcolex, and longcolex):
>>> Pythons(['Idle']).shortlex() < Pythons(['Palin']).shortlex()
TrueSorting a collection of bitsets without using a key function will order them in colexicographical order.
Powersets
Iterate over a bitsets’ powerset in short lexicographic order:
>>> for p in Pythons(['Palin', 'Idle']).powerset():
... print(p.members())
()
('Idle',)
('Palin',)
('Idle', 'Palin')frozenset compatibility
For convenience, bitsets provide the same methods as frozenset (i.e. issubset, issuperset, isdisjoint, intersection, union, difference, symmetric_difference, __len__, __iter__, __bool__, and __contains__).
>>> 'Cleese' in Pythons(['Idle'])
False
>>> 'Idle' in Pythons(['Idle'])
True
>>> Pythons(['Chapman', 'Idle']).intersection(Pythons(['Idle', 'Palin']))
Pythons(['Idle'])Note, however that all the operators methods (+, -, &, | etc.) retain their integer semantics:
>>> print(Pythons(['Chapman', 'Idle']) - Pythons(['Idle']))
1In tight loops it might be worth to use bitwise expressions (&, |, ^, ~) for set comparisons/operations instead of the frozenset-compatible methods:
>>> # is subset ?
>>> Pythons(['Idle']) & Pythons(['Chapman', 'Idle']) == Pythons(['Idle'])
TrueAdded functionality
Differing from frozenset, you can also retrieve the complement set of a bitset:
>>> Pythons(['Idle']).complement()
Pythons(['Chapman', 'Cleese', 'Gilliam', 'Jones', 'Palin'])
>>> Pythons().complement().complement()
Pythons()Test if a bitset is maximal (supremum):
>>> Pythons(['Idle']).all()
False
>>> Pythons(['Chapman', 'Cleese', 'Gilliam', 'Idle', 'Jones', 'Palin']).all()
TrueTest if a bitset is non-minimal (infimum), same as bool(bitset):
>>> Pythons(['Idle']).any()
True
>>> Pythons().any()
FalseVisualization
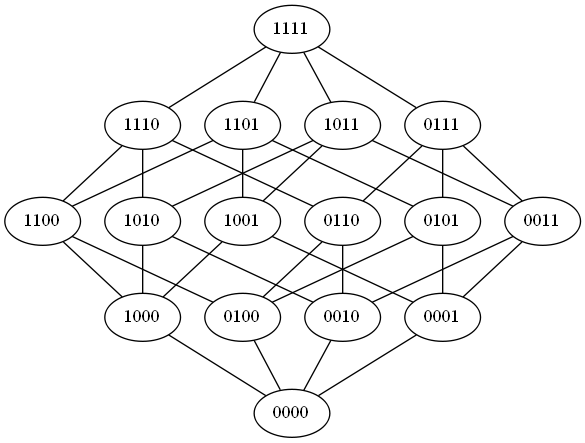
With the help of the optional Graphviz graph layout library and this Python interface, the bitsets.visualize module can create Hasse diagrams of all bitsets from your domain:
Download and install Graphviz. Then install the Python interface:
$ pip install "graphviz>=0.3, <0.4"Make sure that the bin directory of Graphviz is on your system path.
>>> from bitsets import visualize
>>> Four = bitset('Four', (1, 2, 3, 4))
>>> dot = visualize.bitset(Four)
>>> print(dot.source) # doctest: +ELLIPSIS, +NORMALIZE_WHITESPACE
// <class bitsets.meta.bitset('Four', (1, 2, 3, 4), 0x..., BitSet, None, None)>
digraph Four {
edge [dir=none]
b0 [label=0000]
b1 [label=1000]
b1 -> b0
b2 [label=0100]
b2 -> b0
b3 [label=1100]
b3 -> b1
b3 -> b2
...
Show members instead of bits:
>>> dot = visualize.bitset(Four, member_label=True)
>>> print(dot.source) # doctest: +ELLIPSIS, +NORMALIZE_WHITESPACE
// <class bitsets.meta.bitset('Four', (1, 2, 3, 4), 0x..., BitSet, None, None)>
digraph Four {
edge [dir=none]
b0 [label="{}"]
b1 [label="{1}"]
b1 -> b0
b2 [label="{2}"]
b2 -> b0
b3 [label="{1,2}"]
b3 -> b1
b3 -> b2
...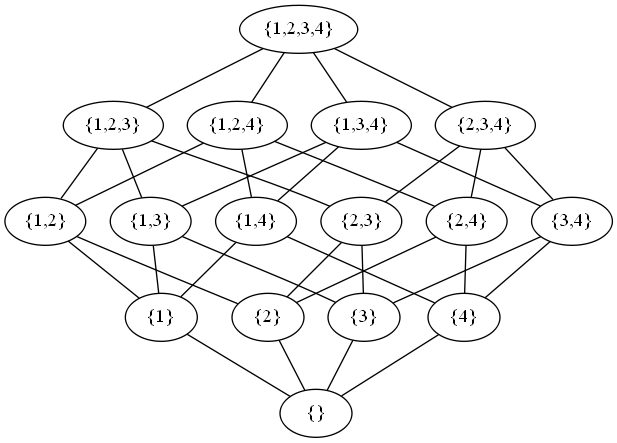
Remember that the graphs have 2 ** domain_size nodes.
Containers
When activated, each bitset class comes with tailored collection classes (bitset list and bitset tuple) for its instances.
>>> Letters = bitset('Letters', 'abcdef', list=True)
>>> Letters.List.frommembers(['a', 'bcd', 'ef'])
LettersList('100000', '011100', '000011')The collection classes have convenience methods for set intersection and union:
>>> import string
>>> Ascii = bitset('Ascii', string.ascii_lowercase, list=True)
>>> ascii = Ascii.List.frommembers(['spam', 'eggspam', 'ham'])
>>> ascii.reduce_and()
Ascii(['a', 'm'])
>>> ascii.reduce_or()
Ascii(['a', 'e', 'g', 'h', 'm', 'p', 's'])Customization
To use a customized bitset class, extend one of the classes from the bitsets.bases module and pass it to the bitset function.
>>> import bitsets
>>> class ProperSet(bitsets.bases.BitSet):
... def issubset_proper(self, other):
... return self & other == self != other
>>> Ints = bitset('Ints', (1, 2, 3, 4, 5, 6), base=ProperSet)
>>> issubclass(Ints, ProperSet)
True
>>> Ints([1]).issubset_proper(Ints([1, 2]))
True
>>> Ints([1, 2]).issubset_proper(Ints([1, 2]))
FalseTo use a customized bitset collection class, extend one of the classes from the bitsets.series module and pass it to the bitset function.
>>> from functools import reduce
>>> import operator
>>> class ReduceList(bitsets.series.List):
... def intersection(self):
... return self.BitSet.fromint(reduce(operator.and_, self))
... def union(self):
... return self.BitSet.fromint(reduce(operator.or_, self))
>>> Nums = bitset('Nums', (1, 2, 3), list=ReduceList)
>>> issubclass(Nums.List, ReduceList)
True
>>> numslist = Nums.List.frommembers([(1, 2, 3), (1, 2), (2, 3)])
>>> numslist.intersection()
Nums([2])
>>> numslist.union()
Nums([1, 2, 3])Note that since version 0.4, this very functionality was added to the bitsets.series classes as reduce_and and reduce_or methods (see above).
Persistence
Bitset classes, collection classes and their instances are pickleable:
>>> import pickle
>>> pickle.loads(pickle.dumps(Pythons)) is Pythons
True
>>> pickle.loads(pickle.dumps(Pythons()))
Pythons()
>>> pickle.loads(pickle.dumps(Pythons(), protocol=pickle.HIGHEST_PROTOCOL))
Pythons()
>>> pickle.loads(pickle.dumps(Letters.List)) is Letters.List
True
>>> pickle.loads(pickle.dumps(Letters.List()))
LettersList()As long as customized bitset collection classes are defined at the top-level of an importable module, the class and its instances are pickleable.
>>> pickle.loads(pickle.dumps(Nums.List)) is Nums.List # doctest: +SKIP
True
>>> pickle.loads(pickle.dumps(Nums.List())) # doctest: +SKIP
NumsList()Further reading
See also
License
Bitsets is distributed under the MIT license.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.















